Do třetí části článku o energetickém výdeji městského cyklisty jsem si ponechal faktory, u kterých se vliv na vydávanou energii zjišťuje poněkud obtížněji než v kopcích s jednoduchou rovnicí (E = m . g . h). Kromě exaktních výpočtů si tam budeme muset místy pomáhat kvalifikovanými odhady a úvahami založenými na cyklistické zkušenosti.
Městský cyklista větrem zmítaný
Ještě před otevřením dalších témat ale zpřesním výpočty na základě debaty vedené pod předchozím článkem této série, která se věnovala odporu vzduchu při jízdě na kole (odkaz na přesnější údaje pro odpor vzduchu od uživatele „a-b-c“ zde). Protože odpory vypočtené v minulých článcích přibližně platí pro cyklistu na silničním kole, zkusil jsem odpor vzduchu vypočítat i pro cyklistu na kole městském. Nový výpočet používá následovně upravené hodnoty:
| A | Cd | Cd.A | |
| původní hodnoty | 0,51 | 0,63 | 0,32 |
| silniční cyklista (drops) | 0,32 | 0,88 | 0,28 |
| městský cyklista | 0,70 | 1,15 | 0,81 |
Plocha vystavená větru pro městského cyklistu odpovídá pozici „tops“ na silničce s přidáním cca 10 % za běžné oblečení a brašny. Koeficient odporu vzduchu Cd.A se tak zvýšil cca 2,5 násobně. Pro silniční cyklisty jsem koeficienty také mírně upravil, zde koeficient Cd.A naopak poklesl asi o 10 %.
Přepočet ovlivnil některé závěry ze dvou předchozích článků. Konkrétně požadovaný výkon pro určitou rychlost vzrůstá pro cyklistu na městském kole zhruba na dvojnásobek (viz graf níže) – což snižuje rychlosti dosažitelné na městském kole ve srovnání se silničkou při stejném výkonu zhruba o čtvrtinu. Špičková rychlost „líného“ cyklisty na městském kole tedy je pod 20 km/h.
Závěr ohledně dráhy potřebné k rozjezdu na cestovní rychlost (přibližně 40 metrů) se ale nemění. Vyšší odpor vzduchu městského cyklisty nemá ani velký vliv na efektivitu ve stoupáních nad 3 %, protože se tak děje vesměs v nízkých rychlostech. Ve 3% stoupání při výkonu 200 W poklesne rychlost jen o 2 km/h (z 18 km/h na 16 km/h). Doba k vystoupání 100 metrů se od 3% sklonu také prakticky nemění. Potvrzen zůstává i závěr, že stoupání bývá rychlejší vyšlapat plynule než kombinací trháku a rovinky. Graf rychlostí pro stoupání a výkon platný pro městské kolo má výrazně nižší rychlosti ve stoupáních pod 3 %.
Změní se výsledky výpočtu racionální zajížďky stometrového stoupání. Pro městské cyklisty klesne výhodnost zajížďky zhruba o čtvrtinu, tj. stometrový kopec má smysl na městském kole objet, je-li zajížďka po rovině delší o 3-4 kilometry.
Vane větřík po lučinách mezi paneláky…
O rovinatých zemích se říká, že tam sice nejsou kopce, ale zase je tam vítr. Co tedy udělá s jízdou na kole takový klasický fríský větřík od moře, zdvihající vlny na čtvrtý stupeň Beaufortovy stupnice?
Podívejme se nejprve, o kolik víc vlastně v Dánsku či Nizozemsku fouká. Přímořské státy jsou obecně větrnější, než vnitrozemí. Pro volné plochy ve výšce 10 m nad terénem (tj. letiště) jsem našel jednoduché srovnání, podle kterého je pravděpodobnost výskytu čerstvého větru (20 km/h, 4. a vyšší stupeň Beauforta) v plochých zemích západní Evropy poněkud vyšší než v českém vnitrozemí.
| Síla větru (windfinder.com) | pravděpodobnost větru > 4 beafourt | průměrná rychlost větru (km/h) |
| Praha Kbely | 15% | 13 |
| Brno Tuřany | 24% | 15 |
| Kodaň Kastrup | 50% | 20 |
| Amsterdam Schipol | 47% | 20 |
Jak ukážu níže, protivítr o rychlosti 20 km/h už městského cyklistu na kole prakticky zastaví. Samozřejmě, v ulicích městských center se vítr zpravidla rozptýlí a je slabší než jaký zaznamenají letištní meteostanice. Když to ale od moře fičí padesátkou (podle Meteoblue v Kodani 27 dnů v roce), nebude rozhodně panovat bezvětří ani na kodaňské centrální třídě Ströget.
Modernistická zástavba bohužel nemá na přízemní vítr rozhodně uklidňující vliv. Domy v blocích vítr přechází vrchem, výškové solitéry naopak obchází ze stran. Tím se v prostoru mezi budovami vytváří tryskový efekt, zvyšující rychlost větru v nepříznivých případech i na více než dvojnásobek. A nevadí, že na to poukazoval Jan Gehl v „Životě mezi budovami“ už před čtyřiceti lety. Výšková zástavba, s větrem bičovanými planinami okolo, není na předměstích Kodaně a Amsterodamu rozhodně ničím výjimečným.
Nemusím tedy být daleko od pravdy, když to uzavři tím, že přízemní větry o rychlostech 15 až 20 km/h jsou v Dánsku a Nizozemsku běžné, zatímco v Praze se vyskytují ne sice zcela vzácně, ale rozhodně ne často. Více viz odkazované zdroje Metoblue a WindFinder.
Větrné výpočty
Co se stane, pojede-li cyklista rychlostí 20 km/h proti stejně silnému větru? Silniční cyklista bude muset vydávat namísto 60 wattů hned 275, což je skoro pětkrát více. A cyklista na městském kole, který by toužil vydat se přímo proti větru o rychlosti 20 km/h, se při výkonu 100 wattů prakticky nehne z místa, a na téměř nepoužitelnou rychlost 3,5 km/h musí vydat 150 wattů.
V praxi ale směr větru kolísá, spojuje se s odporem vzduchu daným rychlostí jízdy a výsledný vektor působí na větší plochu než je optimální profil cyklisty prořezávajícího vzduch čelem. V modelu pro boční vítr zavádím ještě proměnnou plochu profilu vzhledem ke směru větru, který je v případě bočního větru 1,5 násobkem profilu cyklisty zepředu (kola, rám, brašny).
Podívejme se tedy, co se stane, bude-li vítr foukat šikmo. Představme si nejprve fiktivního cyklistu na silničce, který bude chtít jet rychlosti právě 20 km/h ve stejně silném větru bez ohledu na jeho směr. Požadovaný výkon bude na směru větru záviset více než výrazně:
Z tohoto grafu plynou jistá zjištění:
- Vítr vanoucí +/- 45° od přímého protisměru má stále velmi podobný vliv jako přímý protivítr.
- Boční vítr, stejně rychlý jako je rychlost jízdy, zvyšuje odpor vzduchu téměř na dvojnásobek. Je to dané tím, že se přidává k odporu vzduchu danému pohybem kola. Působí sice šikmo, ale větší rychlostí a na poněkud větší plochu. Vlivem toho, že odpor vzduchu roste s třetí mocninou rychlosti, to nezachrání ani skutečnost, že vítr vane pod úhlem 45° a jeho výsledná síla je tak pouze 70%.
- Vítr v zádech nemá tak výrazný kladný vliv jaký má protivítr vliv záporný. Ve vyšších rychlostech se již zvyšuje valivý odpor, navíc jízdní kola často nejsou zpřevodovaná tak, aby jezdec mohl vítr v zádech plně využít.
Pojďme ale k městskému cyklistovi s výkonem 100 wattů. Jak jsem již uvedl, vítr o rychlosti 20 km/h mu nedovolí se ani rozjet. Věnujme se tedy větru o něco slabšímu, o rychlosti 15 km/h.
A jaké byly dopady kalkulace na rychlost (v grafu nenápadnou, černou čárou těsně pod červenou linií)?
Za bezvětří by 100 wattů na městském kole stačilo na rychlost zhruba 19 km/h. Proti větru vanoucímu rychlostí 15 km/h pojede se 100 watty jen zhruba šestikilometrovou rychlostí. Bude-li tedy mít cyklista smůlu na protisměrný kvadrant (tedy asi v jednom případě ze čtyř), zapůsobí na něj vítr o rychlosti 15 km/h, jako by se mu silnice zdvihla do 5,5% stoupání. Když se to zprůměruje přes všechny kvadranty, bude vítr působit jako zhruba 1% stoupání.
Obdobné kalkulace jsem provedl pro tři další modelové situace, včetně cyklisty na silničním kole s výkonem 200 wattů. Za zmínku určitě stojí, že zřetelný dopad má už vítr o rychlosti 10 km/h a že vliv větru přepočtený na ekvivalent stoupání slábne s výkonem cyklisty.
| Cyklista | Výkon | Síla větru | Ekvivalent stoupání při jízdě v protivětrném kvadrantu |
| Silniční | 200 W | 20 km/h | 3,3% |
| Městský silný | 150 W | 20 km/h | 12% |
| Městský slabý | 100 W | 15 km/h | 5,5% |
| Městský slabý | 100 W | 10 km/h | 2,5% |
Jízda v provozu
Jízda v provozu vyžaduje rychlost, která z vás neučiní pohyblivý terč a umožní vám třeba zabrat pruh pro odbočení vlevo. Ale jak jsme na tom s naším „městským“ cyklistou, který nechce vydat více než 100 wattů? Tento výkon odpovídá maximální rychlosti 20 km/h. Do té se ovšem bez vydání vyššího výkonu nemáte šanci dostat. A netřeba dodávat, že 20 km/h je rychlost dosti nekomfortní, pokud se máte pohybovat společně s auty jedoucími 50 km/h.
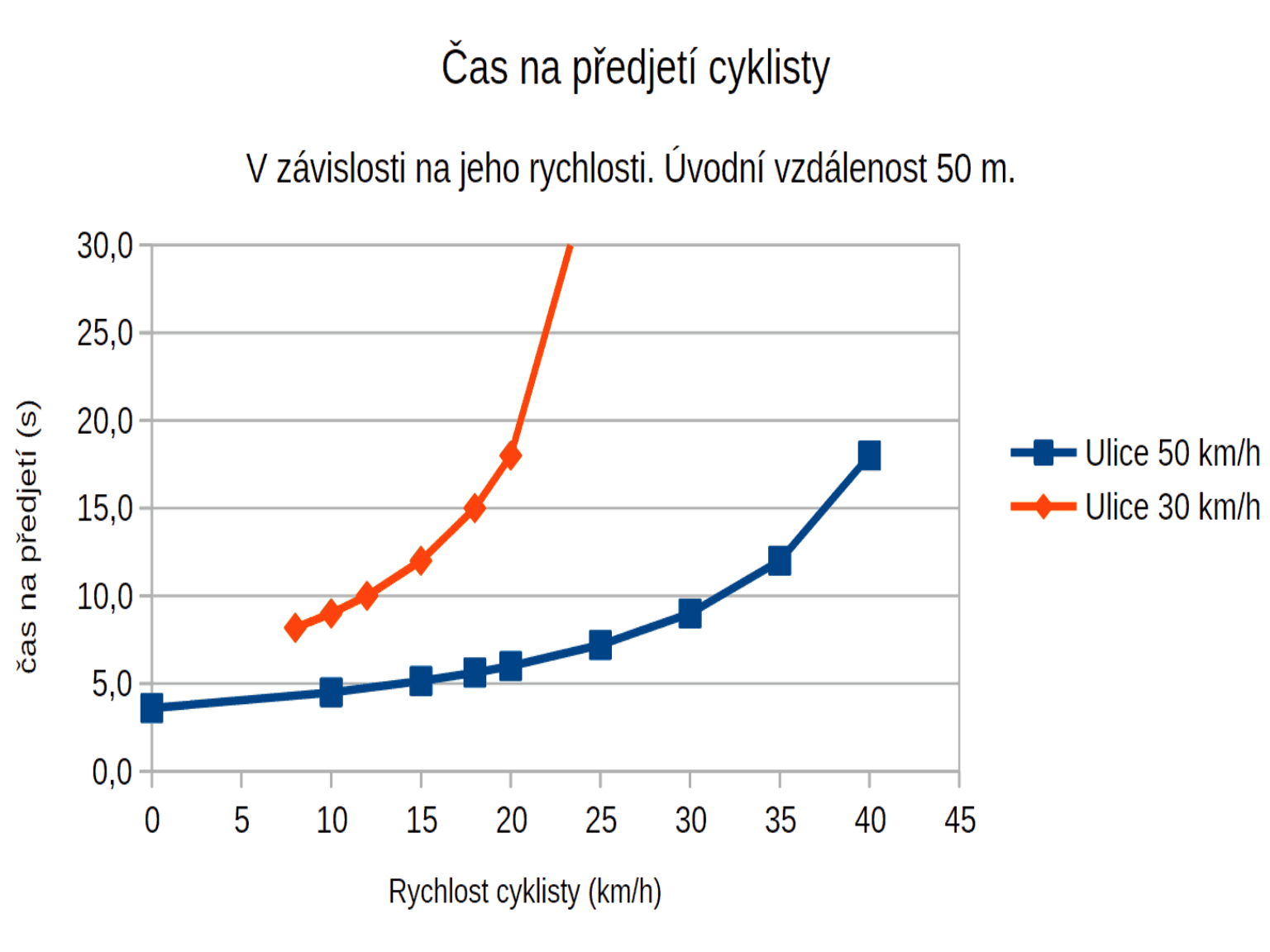
25 km/h je lepší variantou. Svižný cyklista jedoucí 25 km/h dává řidiči na předjetí zhruba o 30 % více času než městský cyklista jedoucí 18 km/h. Zrychlíte-li na 30 km/h, zvětší se čas na předjetí dokonce o 60 % (při zaregistrování cyklisty na vzdálenost 50 metrů je to prodloužení potřebného času z 5,5 na 9 sekund).
(I když to sem tak docela nepatří, tak doplním: Zpomalíte-li na padesátce na 10 km/h – třeba ve stoupání – bude mít řidič na provedení předjížděcího manévru jen polovinu času ve srovnání se situací, kdy jedete třicítkou. Kdyby se ale na ulici omezila rychlost všech vozidel na 30 km/h, získá řidič na předjetí cyklisty naopak minimálně dvojnásobek času oproti situaci, kdy by jel 50 km/h, čímž se problém se zpomalením cyklisty v kopci anuluje. V cykloobousměrce se na vyhnutí získá zklidněním na třicítku o 40 % více času.)
Na udržení rychlosti 25 km/h potřebujete 200 W, ale pro její dosažení musíte pracovat krátkodobě s výkonem vyšším. Samozřejmě je lepší dosáhnout rychlosti přes 30 km/h. V té se již pruhy zabírají celkem snadno, stejně tak se hravě udržíte v poskakující koloně. Při rychlosti přes 30 km/h tím ale i na silničním kole přecházíte do sféry „200 W pro udržení rychlosti, o akceleraci nemluvě.“ Zkrátka a dobře, v provozu s auty jako cyklista závodíte, i když se vám vůbec nechce.
Kdo si troufne v silnějším provozu jet způsobem, který zachová výdej energie do 100 W, tedy pod 20 km/h bez silné akcelerace a trvalého cukání zrychlit někam ke třicítce, ten může rovnou od zítřka nastoupit na pozici po Gándhím.
A samozřejmě, jakmile k tomu přibude několik procent stoupání, je to s línou jízdou v provozu definitivní konec. Cyklista, který nechce spáchat sebevraždu, se proto buďto dobrovolně vybičuje ke sportovnímu výkonu vysoko přes 200 W, nebo zbaběle prchne na chodník.
Dlažba (a pláště)
Jak je patrné ze vzorce v prvním článku, odpor z tření se vyjadřuje koeficientem valivého odporu. Pro silniční kolo na asfaltu se uvádí koeficient cca 0,004. Hladšími povrchy je jen hlazený beton nebo palubovka cyklistického oválu. Pro nerovnější povrchy, jako třeba hrubě zpevněná či dlážděná silnice se uvádějí koeficienty až po 0,010.
Pro další úvahy je dobré vědět, že každých 0,010 v koeficientu valivého odporu odpovídá zhruba 1% stoupání.
Věc ale není tak jednoduchá. Valivý odpor i na relativně hladkém povrchu závisí na šířce a typu plášťů. Měření valivého odporu v závislosti na typu plášťů ukazuje, že široké balonové pláště mohou mít na hladkém povrchu, oproti užším plášťům silničním či turistickým, odpor i více než dvojnásobný. Závisí také na nahuštění. A podstatný vliv na komfort jízdy má, nakolik se na kolo či cyklistu přenášejí vibrace z nerovného povrchu. To nezáleží jen na pláštích a tlaku v pneumatikách, ale také na odpružení kola. V rámci teorie to můžeme všechno schovat do koeficientu valivého odporu, který pak ale rozhodně poroste vysoko přes oněch zmiňovaných 0,010 odpovídajících 1% stoupání. (link1, link2, link3)
Jak moc mohou udělat vibrace, vyzkoušeli redaktoři Bicycle Quaterly (link). Test se silničními plášti v rychlosti 26 km/h na obdobě dlažebních kostek prokázal, že nutný výkon může být až více než dvojnásobný (473 vs. 183 W). V tomto případě, kdy byl pro nerovný povrch vybrán úmyslně zcela nevhodný plášť, činil vliv hrubého povrchu ekvivalent až 4% stoupání.
Vibrace kola a jejich tlumení cyklistou jsou rozhodně nezanedbatelným vedlejším efektem pražských dlažebních kostek. Samotný koeficient valivého odporu tak k vyjádření dopadu dlažebních kostek na požadovaný výkon cyklisty rozhodně nestačí.
I tak se dá ale pro městská neodpružená kola odhadnout, že na užších pláštích se koeficient valivého odporu vlivem vibrací celého kola a jezdce posouvá někam k 0,03 až 0,04 (ekvivalent 3-4% stoupání). I na širokých pláštích, které mají na hladkém asfaltu nejspíš kolem 0,01, neporoste koeficient valivého odporu méně než k 0,02 (ekvivalent 2% stoupání). Silnější pláště, hustí-li se kvůli komfortu na dlažbě na minimum, mají zase nevýhodu ve větším valivém odporu na rovném povrchu.
Zkrátka a dobře, kočičí hlavy vám udělají z rovinky kopec. A z mírného kopce kopec strmý.
Pro ověření těchto odhadů by bylo velmi zajímavé vyrazit do Prahy na kole s tenzometrem a reálně změřit výkon pro zachování rychlosti 20 km/h na asfaltu, malých kostkách, rovných kočičích hlavách a „známých“ hlavách křemencových, a to v rovině a případně i v různých sklonech. Diplomová práce pro Fakultu dopravní jak stvořená.
V závěrečném článku shrneme z hlediska potřebného výkonu typické situace na komfortní infrastruktuře i v pražské realitě a pustíme se do závěrů.
Užitečné odkazy
https://janheine.wordpress.com/2012/08/12/suspension-losses/
https://janheine.wordpress.com/2016/06/14/suspension-losses-confirmed/
http://www.analyticcycling.com/DiffEqMotionFunctions_Page.html
http://www.arch.ksu.edu/seamon/fajans.htm
http://www.amler.biz/fyzika/auto/
https://www.gribble.org/cycling/power_v_speed.html
http://www.cyclingpowerlab.com/CyclingAerodynamics.aspx
http://www.analyticcycling.com/DiffEqMotionFunctions_Page.html
http://www.sciencedirect.com/science/article/pii/S1877705812016955
http://people.cst.cmich.edu/yelam1k/asee/proceedings/2015/Paper%20files/Student_Papers/2015_ASEE_NCS_Conference_submission_61.pdf










Nightrider 28. 8. 2017, 09:37
Kočičí hlavy jsou vůbec kapitola sama pro sebe, hlavně pro menší kola. Abych nerozbil náklad, musím zpomalit do kroku. Abych neulomil sedlovku, musím šlapat vestoje. A místo sledování okolního provozu musím sledovat silnici a kličkovat mezi dírami. Za mě tedy radši dva kilometry a kopec navíc, než sto metrů kostek.
vlákno 28. 8. 2017, 14:24
široké balonové pláště mohou mít na hladkém povrchu, oproti užším plášťům silničním či turistickým, odpor i více než dvojnásobný. Závisí také na nahuštění.
To je trochu zavádějící výrok, protože při stejném nahuštění má širší plášť menší valivý odpor než užší plášť (za jinak stejných podmínek). Takže nahuštění je zcela zásadní, rozhoduje o tom, jak velká plocha pláště je na styku s povrchem a kolik ztratí kolo na své "kulatosti".
DJ 28. 8. 2017, 16:56
S tím větrem mi přijde, že jste správnou metodikou přišli k divným výsledkům. Delší poryv protivětru okolo 10 m/s (znásobený vysokou budovou) mě na kole se „střední“ (řekněme trekovou) pozicí a při klidném šlapání zpomalí z 25 na 10–15 km/h. Při protivětru 20 km/h tedy nevidím důvod, proč by rychlost městského cyklisty měla klesnout níž (má sice horší Cx.A, ale protivítr je zase o dost slabší).
Jinak v silném větru vypadá jako velká výhoda, když je kolo těžké, srovnejte tahle videa s plus minus podobnou rychlostí větru:
https://www.youtube.com/watch?v=93sx0lpxqI4
https://www.youtube.com/watch?v=c75b_98q-0c
:)
Vratislav Filler 28. 8. 2017, 22:09
vlákno: Jo, ta formulace se úplně nepovedla. Vychází se z toho, že široké pláště se foukají na menší tlaky, zvlášť, chceme-li komfort na kostkách. Nechtěl jsem se pouštět do komplikovaných vztahů valivého, a aerodynamicého odporu u různě širokých plášťů, jakož i do toho, co s tím udělá vzorek.
DJ: Zajímalo by mě, zda tam mám něco špatně (jak jste měřil těch 10 m/s?)
Vratislav Filler 28. 8. 2017, 22:10
DJ: No, když to ultralehké kolo vítr prostě odfoukne, to se na něj dá nasednout dost těžko ;-)
DJ 29. 8. 2017, 23:53
VF:
1) nevím, čas přechroupat čísla sám nemám, tak jen přidávám praktickou zkušenost. Rychlost beru z Aladina, vzhledem k tomu, že tyhle zážitky mám z blízkosti 18patrového věžáku (s téměř dokonalou rovinkou), spíš bude reálná rychlost větru ještě výš.
2) Jo. Těžko pak optimalizovat kolo zároveň na vítr a kopce. :)
MM 30. 8. 2017, 09:16
Doplnění velocipédu o vhodnou motorovou jednotku vyřeší oba problémy naráz:-). A netřeba zůstat jen u toho ... ;-)
Vratislav Filler 30. 8. 2017, 12:27
DJ: 1) Napadá mě jedině, že v tom protivětru začne člověk podvědomě víc šlapat, takže výkon jde nahoru, rychlost dolů a pak by to vycházet mohlo.
Jan Herda 30. 8. 2017, 20:47
Myslím že tyto laboratorně-předvídatelně (z)kreslené grafy nám spíš kazí radost z jízdy :-) Ano, kopce brzdí, stejně tak protivítr, povrch ..., ale taky náklad na zádech, semafory, nutné zajížďky atd. Koeficienty se mi ani teď úplně nelíbí - že bych jel na silničce s 85W 25km/h? Po čtvrt milionu km ohnutý za řídítky silničky vím, že v ČR nefouká skoro nikdy tak aby se nedalo jet 20kou po rovině (když sypeš 250W) stejně tak i 8% kopec se přejede hlavně pokud člověk "není tlustej". Bohužel je třeba si uvědomit, že v džínách a mikině na městském kole nejde jezdit aniž bych se nezapotil jinak než "po rovině pomalu". Pro delší přesuny je zapotřebí cyklistický ohoz a pokud možno sportovní kolo a asfalt. Ad kostky - nejlíp se přeletí 40kou, už 30km/h je málo :-)
a-b-c 31. 8. 2017, 12:44
Jan Herda:
Koeficienty se mi také úplně nesedí. V tom odkazu je víc možností.
Horní tabilka mi přijde u oblouků dost odvážná, ale níž jsou interaktivní políčka pro odhad koeficientů a těm věřím o něco víc než té tabulce.
Když při použití koeficientů z toho odhadu to hází podle vzrůstu a váhy cyklisty něco kolem
25 km/h => 120 W
30 km/h => 200 W
35 km/h => 290 W
40 km/h => 410 W
Wattmetr nemám, takže si to srovnat nemůžu. Také jezdím na silničce, ale Vaše objemy najeté nemám. Nicméně tohle už mi přijde reálnější.
Ps. Grafem si radost z jízdy kazit nenechám, ale hledání proč to nesedí ke zkušenostem mě baví...
DJ 1. 9. 2017, 12:17
VF: když mám sportovní náladu, tak jo, ale když ne, tak holt řadím níž, nahnu se dopředu, a akceptuju, že velocipéd je asi nejmíň aerodynamickej dopravní prostředek. :)
Jan Herda: s tou nutností silničky a cyklobuznovskýho vohozu mě stejně trochu iritujete. :) Po dnešních 25 km na rekole můžu zodpovědně říct, že i tahle vzdálenost je na městském kole v pohodě, a ani mě to oproti mýmu kolu moc nezpomalilo (průměrná ~17 km/h místo 20–22, co v městským provozu jinak dosahuju).
Vysvětlitelný je to vcelku jednoduše:
• aerodynamický odpor se snižující se rychlostí hodně rychle klesá
• nižší nebo vyšší maximálka mívá na průměrnou rychlost minimální vliv (extrémní příklad: jdete do hospody 4 km za 1h, zpátky vás přemístí teleportem ze startreku, tím se průměrná rychlost zvedla na závratných 8 km/h)
• na rekole mi líp vycházejí semafory, podstatně míň času tak pro…stojím :) na červených.
Velkej bonus městskýho kola pak je viditelnost, ve vzpřímené pozici je mnohem snazší si udržet přehled o provozu za sebou
Jan Herda 5. 9. 2017, 11:20
Tak exaktní záznam ze silničky - wattmetr Powertap G3 - 21km v lehce zvlněném terénu s převýšením 170m - průměrná rychlost 30km/h, nutný výkon 185W - 8kg karbon silnička + 70kg jezdec, lehce foukalo, jelikož to byl okruh tak by se měl vliv větru de facto (skoro) vyrušit. Rozjezd aby to bylo svižné 400+. Včerejšek v Krkonoších - kopec 6% ze Svobody n/úpou na Hoffmanky průměr 17,9km/h 270W, kopec 4% z Fořtu přes černý důl na Hoffmanky 19,5km/h a 233W průměr. Kámoš co má 85kg musí na stejnou rychlost dávat v kopci 340W , 293W. Pokud jedu (skoro doraz) 9% svižně 14,5km/h tak dávám 320W. Ohledně roviny - cca 110W na těch 25km/h ale čísla se rychle mění a stačí si jednou přišlápnout a je tam 200, naopak po 250 se člověk cítí unaven i 120W pár vteřin. Provoz bohužel není zcela plynulý, tudíž člověk si pořád přišlapává, brzdí, do toho vítr ... proto jsou laboratorní výsledky skoro nepoužitelné pokud nejede na prázdné stezce do Bráníka za bezvětří, které stejně nikdy není :-) Pokud budu mít čas zkusím vyzobat ze záznamu ještě něco, ale musím Powertap vrátit a do městského provozu ho nevezmu.
Ivoš 16. 10. 2017, 12:01
S tím protivětrem vám vychází podivné výsledky. Lidé neumí počítat, na to jsem zvyklý, ale vám nepřijde divné, že výsledky jsou zcela mimo zkušenosti z vlastního ježdění?
Pro jednoduchost zanedbávám ostatní, odpor vzduchu je dominantní.
P = Cd.A * V3 je zjednodušením, které platí pro bezvětří.
Pro protivítr je to potřeba počítat:
P = F (síla/odpor) * d (dráha za jednotku času/rychlost)
F = Cd.A * (Vv + Vc)2
d = Vc
P – Výkon
Vc – Rychlost cyklisty
Vv – Rychlost větru
Dohromady
P = Cd.A * (Vv + Vc)2 * Vc
Z uvedeného vychází, že proti větru 15 km/h klesne rychlost z 19 na 10,5 km/h a nikoliv 6 km/h, jak je uvedeno v článku.
(Resp. proti větru 20 km/h klesne rychlost z 20 na 9,4 km/h a nikoliv 3,5 km/h, jak je uvedeno v článku.)
I městský cyklista mívá mozek, takže se sehne a sníží plochu, k tomu o čtvrtinu zvedne výkon a jede cca 14 km/h. Pokud fouká víc, sehne se víc :-)
Takto to alespoň vypadá u mě.
Dále: je hezké, že máme přesná data pro vítr 10 m nad terénem otevřeného letiště. Já jezdím mnohem blíže povrchu a v případě městského kola často po městě. V Praze je 95% času vítr zanedbatelný. V české krajině je 85% času vítr faktor, ovlivňující rychlost do 10%. To není vědecký výpočet, ani odborné měření, ale laická zkušenost z mnohaletého pravidelného ježdění.